Sort your raw data, and write the sorted data here.
データを順序に並べてここに書くこと。
[16, 18, 19, 21, 21, 22, 22, 22, 24, 25]
Convert your data to “subjective sizes,” and enter the absolute, relative, and cumulative relative frequency distributions here. What is the median of your data?
データを「主観的サイズ」に変換して絶対頻度分布、相対頻度 分布、または(相対)累積分布を書け。中央値(メディ アン)はどれですか?
Label Up to Value Frequency Relative CDF
very small 19.5 18 3 0.3 0.3
small 22.5 21 5 0.5 0.8
large 25.5 24 2 0.2 1.0
very large infinity 27 0 0.0 1.0
Sample answer: The median is [21, 22]. (This is the median of the raw data, and may contain one or two values because there is an even number of observations. You may also have computed the median of the distribution, which was ['small']. Since I didn't specify carefully, that is also OK, as long as your computation is clear.)
For each “subjective size,” choose a representative numerical size. Enter the correspondence here. Explain why you chose each numerical value.
各「主観的サイズ」に代表的量的サイズを選んで、こ こに記入。それぞれの値を選んだ理由を説明せよ。
Sample answer: The representative sizes are listed in the "Value" column in the table in the preceding answer. The values for "small" and "large" were chosen as the midpoints of the range. The values for "very small" and "very large" were chosen to have equal distances between the representative values. This would work well if sizes are normally distributed with a mean in the "small" to "large" range, and a standard deviation of 3-5 students.
You may have chosen different values. That is OK. I will evaluate your answer based on your explanation, not on whether you chose the same values that I did here.
Using the representative sizes you chose in the previous problem, compute the mean, variance, and standard deviation of the distribution of sizes. Show your work (e.g., using a table like that in Homework 2's spreadsheet).
前の問題で選んだ代表的サイズと分布を用いてサイズ分布の 平均値、分散、と標準偏差を計算 せよ。計算方法を表すテーブルなどを含むこと。(たとえ、第2 宿題のシートのようなもの。)
Sample answer:
mean = 20.70
variance = 4.41
standard deviation = 2.10
Pick one of the following three cases, and answer the question in the space provided below.
以下の状況説明から一つを選んで、下記の問aと問bを答えろ。
-
The data set of class sizes was derived from the daily attendance over a 10-day period in March 2010 at one kindergarten somewhere in Tsukuba City.
クラスサイズデータは2010年3月の10日間分のあるつくば 市の幼稚園の日次出席データである。
-
The data set of class sizes was derived from the lists of registered students on March 1 of each year in a 10-year period at one kindergarten somewhere in Tsukuba City.
クラスサイズデータは3月1日付の10年間分のあるつくば市の 幼稚園の年次登録(学生名簿)データである。
-
The data set of class sizes was derived from the lists of registered students on March 1 of 2010 at 10 different kindergartens in Tsukuba City.
クラスサイズデータは3月1日付の10ヵ所分のつくば市にある 幼稚園の年次登録(学生名簿)データである。
For your chosen case, give one example of a “hidden factor” relating different observations in the data set that could affect the way you interpret your statistics. Explain why this matters.
選択状況には「隠された要因」により観察間関係が現れ、統計量 の解釈に影響を及ぼすことがある。その要因・関係をひと つを選んで説明せよ。
Sample answer: We give an answer for each case. You should compare to the case you chose. Note that these are examples only; there may be others.
In the case where data was attendance on ten consecutive days, here are four factors to consider.
Some children are probably absent on any given day, but the class size must be regulated for the case when all children are present. Attendance is a biased estimator for class capacity.
A child who is sick is reasonably likely to be sick for a few days running. Observations are unlikely to be independent from day to day.
In the case of contagious diseases like influenza, if one child gets sick, it's likely that others will get sick, too. Observations are unlikely to be independent from day to day.
Because all observations relate to one group of children in one year, trends cannot be observed and forecasts are hard to make.
In the case of a single kindergarten observed for ten years, here are two factors to consider.
Since only one school is observed, it may not be representative.
Because the school is observed over several years, trends in attendance can be observed and used to forecast future class sizes.
In the case of ten kindergartens observed in a single year, trends cannot be observed and forecasts are hard to make.
A group of parents complained to the Tsukuba City Board of Education about class sizes. The Board is considering prohibiting very large classes, i.e., classes with 26 or more students. Assume your data is based on the registration lists of a sample of 10 different kindergartens in Tsukuba City.
つくば市教育委員会がある両親のグループからクラスサイズに ついての文句を受け、大きすぎる(「非常に大きい」)クラスを 禁止する案を検討する。クラスサイズデータセットAは3月1日 付の10年間分のあるつくば市の幼稚園の年次登録(学生名簿) データとする。
-
Based on your Data Set A, do you think there is a problem related to class size? Explain why or why not, based on statistics you compute in Problem 4.
問題があるかどうかをデータセットAに基づいて検討せよ。 問4で計算した統計量に基づき理由を説明すること。
Sample answer: The logic here is based on the distance of the boundary (25) above the mean, measured in units of the standard deviation, which allows us to estimate the probability of a given class being “very large,” which we assume is a problem. The problem may be educational or “political” (i.e., a matter of the parents' perception), but we assume the Board will want to “do something” about it. That is sort of a common sense assumption you do not have to justify. The specific numerical arguments below are given for concreteness (and because they make it possible for me to write a program to decide how to explain your individual data), but you are not expected to know them, just to make your judgment based on number of standard deviations.
More than 5% of classes may be expected to be very large (according to the normal approximation, Φ(25) < .95 since (25 - μ)/σ = 1.56 < 1.7). This indicates that there is likely to be a problem.
-
Based on your Data Set A, do you think the proposed regulation limiting class size to 25 or less will change the distribution of class sizes in Tsukuba? Explain why or why not.
データセットAを参照して過大クラス禁止案はつくば市の 幼稚園クラスサイズ分布に大きい影響が与えられるかにつ いて自分の意見を述べてその理由を説明せよ。
Sample answer: The logic here is based whether the boundary of very large classes (25) is above or below the largest class size observed. (However, you could also make a statistical argument similar to the above, and say that if the boundary is “many” standard deviations above the mean, the distribution won't change “very much.” In statistical terms, the difference of two distributions is measured by the amount of “movement among cells,” and if 1% or less of classes move from “very large” to “large,” that is a “small” change.)
No current classes are very large. Since the new regulation would prohibit very large classes, it is very unlikely that the distribution will change. (Note that even if no classes fall into the “very large” category in the future, the distribution among smaller categories could change radically.)
For Problems 7 and 8, use Data Set B. (Each student receives a different data set.) Data Set B is a data set of examination scores on a 0-100 scale.
問題7・8にデータセットBを利用してください。(注意: 皆に別のデータを用意する。必ずデータセットIDを確認すること。) データセットBはある試験の点数データで、0〜100の範囲である。
Copy your data set here:
ここにデータを写ってください:
[100, 63, 100, 92, 90, 100, 82, 54, 81, 100]
Give the definition of mode. Find the mode of the raw data from Data Set B. Now, convert Data Set B to letter grades according to the usual scale, and enter a table containing the letter grade, the scale interval, the absolute frequency, the relative frequency, and the cumulative frequency distribution. What is the mode of the distribution of letter grades? Compare it to the raw (point score) mode.
最頻値(モード)の定義を書け。データセットBの最頻値を記入 せよ。データセットBを普通のスケールでレターグレードに変換 し、レターグレード、スケール範囲、絶対同数、相対同数、と (相対)累積頻度分布を表に記入すること。レターグレード分布 の最頻値を求めよ。点数のモードと比較せよ。
Sample answer: The mode is the value that occurs most frequently in a data set or distribution. The mode of the raw data set is [100]. (There may be multiple values.)
Label Up to Value Frequency Relative CDF
D 60 55 1 0.1 0.1
C 70 65 1 0.1 0.2
B 80 75 0 0.0 0.2
A 100 85 8 0.8 1.0
The mode of the distribution is ['A']. (There may be multiple values.)
Draw a histogram for the raw data set. Drawing a histogram involves a choice of division into cells of values. (Recall that a cell is a group of values that are close to each other.) Explain why you chose the cells you did.
点数データのヒストグラムを描け。ヒストグラムの作成には値の 区間(セル、仕切り)の選択が必要だ。(区間は値の範囲だ。) 区間の選択の理由を説明せよ。
Sample answer: Any of the following three histograms, with the explanation, would be satisfactory.
|XXX|
|XXX|
|XXX|
|XXX|
|XXX|
|XXX|
|XXX|
|XXX||XXX| |XXX|
--------------------
D C B A
The histogram above uses the "standard" letter grade cells (left-to-right they are 0-60 = "D", 61-70 = "C", 71-80 = "B", and 81-100 = "A"). This histogram presents the success level of the students in the class in the usual terms, i.e., as letter grades. Because there are so few cells, it is not very good at presenting outliers, and may tend to make the values appear to be more evenly distributed than they actually are. Note: Due to the method of generating the histogram, my graph does not adjust frequencies to densities. This is incorrect. The adjustment should be done when drawing a histogram for these cells using numerical values!
|XXX|
|XXX|
|XXX||XXX|
|XXX||XXX|
|XXX||XXX| |XXX||XXX|
--------------------------------------------------
> 0 >10 >20 >30 >40 >50 >60 >70 >80 >90
The histogram above divides the numerical scores into ranges of 10. It is a good compromise between the other two, if you want to capture outliers, but also have a fairly "smooth" display of the distribution.
X
X
X X
X X X XX X
--------------------------------------------------
1 2 3 4 5 6 7 8 9 1
0 0 0 0 0 0 0 0 0 0
0
The histogram above divides the numerical scores into ranges of 2. This gives a very sparse picture, and doesn't really reflect how smooth the underlying distribution of human ability is.
What are the values of
- skewness
- kurtosis
for the standard normal distribution?
標準正規分布の
- 歪度(スキューネス)
- 尖度(クルトシス)
の値を書け。
Sample answer: skewness = 0, kurtosis = 3.
Sketch the graph of the cumulative distribution function of a standard normal random variable. Label the axes with correct numerical values (you should know at least 3).
標準正規確率変数の累積分布を描け。(大体で も良い。)軸の数量的な値でラベルを記入すること。(目標は3つ 以上。)
Sample answer:
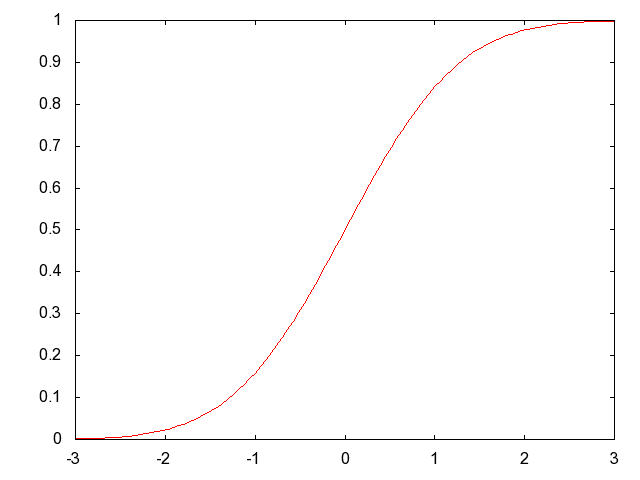
In the graph above you should be able to identify the CDF extreme values 0 and 1, and the midpoint &Phi(0) = 0.5. Some students (especially those with previous exposure to statistics) may have been able to identify Φ(-2.3) = 0.01, Φ(-1.7) = 0.05, Φ(1.7) = 0.95, and Φ(2.3) = 0.99.
Class B of the 3rd grade in East Takezono Elementary School is supposed to be the most international class in Tsukuba City, in terms of nationality of its students. Take a student from Class B at random, and consider the events A = “the student is Chinese,” and B = “the student is female.” State as many facts as you can about Pr({}), Pr(A), Pr(B), Pr(A ∩ B), Pr(A ∪ B), and Pr(Ω), including comparing the probabilities of two events (e.g., Pr(A) < Pr(Ω)).
つくば市のもっとも国際的な年度組は竹園東小学校の3年B組と言われてい る。つまり、生徒の国籍が一番多い。ランダムにB組のひとりの生徒を選出 し、A=「中国人だ」とB=「女性だ」という事象を考察しよう。 Pr({})、Pr(A)、Pr(B)、Pr(A ∩ B)、Pr(A ∪ B)、Pr(Ω) についてできるだけ多くの事実を書け。事象の確率の比較を含む。(例: Pr(A) < Pr(Ω)。)
Sample answer: Based on common sense we assume that some but not all of the students are female, and that some but not all of the students are Chinese. If you do not make this assumption, just change the inequalities in the first two lines to ≤.
0 = Pr({}) < Pr(A) < Pr(&Omega) = 1
0 = Pr({}) < Pr(B) < Pr(&Omega) = 1
Pr(A) = Pr(A ∪ {}) = Pr(A ∩ Ω)
Pr(B) = Pr(B ∪ {}) = Pr(B ∩ Ω)
Pr(A ∩ B) ≤ Pr(A) ≤ Pr(A ∪ B)
Pr(A ∩ B) ≤ Pr(B) ≤ Pr(A ∪ B)
Again based on common sense it seems reasonable to guess that
Pr(A) < Pr(B)
but this is less certain.